（本小题共12分）已知焦点在
轴的椭圆
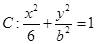
的左、右焦点分别为
，直线
过右焦点
，和椭圆交于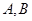
两点，且满足
，直线的斜率为
．
（1）求椭圆C的标准方程；
（2）设F为椭圆C的右焦点，T为直线
上纵坐标不为0的任意一点，过F作TF的垂线交椭圆C于点P，Q．
（ⅰ）若OT平分线段PQ（其中O为坐标原点），求
的值；
（ⅱ）在（ⅰ）的条件下，当
最小时，求点T的坐标．
上随机取一个数
，则
的值介于
到
的概率是
,
，
，求
的最大值
，及
，求
（
）最小正周期是
，求函数
的单调递增区间.
={
︱
},
={
且
}
Ø,求
的取值范围推荐套卷
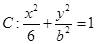
（本小题共12分）已知焦点在轴的椭圆 的左、右焦点分别为，直线过右焦点，和椭圆交于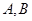两点，且满足，直线的斜率为 ．
（1）求椭圆C的标准方程；
（2）设F为椭圆C的右焦点，T为直线上纵坐标不为0的任意一点，过F作TF的垂线交椭圆C于点P，Q．
（ⅰ）若OT平分线段PQ（其中O为坐标原点），求的值；
（ⅱ）在（ⅰ）的条件下，当最小时，求点T的坐标．
粤公网安备 44130202000953号