已知：∠MON=40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O 重合），连接AC交射线OE于点D．设∠OAC=x°．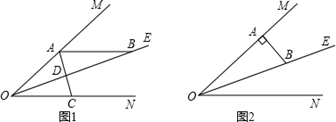
（1）如图1，若AB∥ON，则：
①∠ABO的度数是 ；
②当∠BAD=∠ABD时，x= 120°
；当∠BAD=∠BDA时，x= 60°
．20°；
（2）如图2，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，求出x的值；若不存在，说明理由．
相关试题
如图, 在正方形网格中，△ABC的顶点和O点都在格点上．
（1）在图1中画出与△ABC关于点O对称的△A′B′C′；
（2）在图2中以点O为位似中心，将△ABC放大为原来的2倍(只需画出一种即可).
抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
| x |
… |
－2 |
－1 |
0 |
1 |
2 |
… |
| y |
… |
0 |
－4 |
－4 |
0 |
8 |
… |
（1）根据上表填空：
①抛物线与x轴的交点坐标是和；
②抛物线经过点(-3, )；
③在对称轴右侧，y随x增大而；（2）试确定抛物线y=ax2+bx+c的解析式.
相关知识点
推荐套卷
粤公网安备 44130202000953号