先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2-6n+9=0,求m和n的值.
解:∵m2+2mn+2n2—6n+9=0
∴m2+2mn+n2+n2-6n+9=0
∴(m+n)2+(n-3)2=0
∴m+n=0,n-3=0
∴m=-3,n=3
问题:(1)若x2+2y2-2xy+4y+4=0,求xy的值.
(2)已知△ABC的三边长a,b,c都是正整数,且满足a2+b2-6a-6b+18+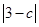 =0,请问△ABC是怎样形状的三角形?
=0,请问△ABC是怎样形状的三角形?
先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2-6n+9=0,求m和n的值.
解:∵m2+2mn+2n2—6n+9=0
∴m2+2mn+n2+n2-6n+9=0
∴(m+n)2+(n-3)2=0
∴m+n=0,n-3=0
∴m=-3,n=3
问题:(1)若x2+2y2-2xy+4y+4=0,求xy的值.
(2)已知△ABC的三边长a,b,c都是正整数,且满足a2+b2-6a-6b+18+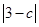 =0,请问△ABC是怎样形状的三角形?
=0,请问△ABC是怎样形状的三角形?