如图，△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．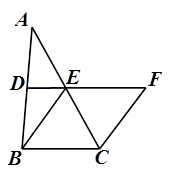
（1）求证：四边形BCFE是菱形；
（2）若CE=8，∠BCF=120°，求菱形BCFE的面积．
相关试题
，
，
，
1－
＋
＋
＝1－
.
＝ ；
＋…＋
； 
； 
； 
×30（用简便方法计算）；
，22，
，
，0，
，—2012 
，1，并比较它们的大小，将它们从小到大的顺序用“＜”连接．
相关知识点
推荐套卷
如图，△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．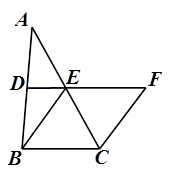
（1）求证：四边形BCFE是菱形；
（2）若CE=8，∠BCF=120°，求菱形BCFE的面积．
粤公网安备 44130202000953号