(本小题满分13分)已知函数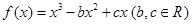 ,其图象记为曲线
,其图象记为曲线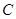 .
.
(Ⅰ)若 在
在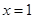 处取得极值为
处取得极值为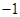 ,求
,求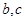 的值;
的值;
(Ⅱ)若 有三个不同的零点,分别为
有三个不同的零点,分别为 ,且
,且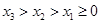 ,过点
,过点 作曲线
作曲线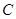 的切线,切点为
的切线,切点为 (点
(点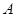 异于点
异于点 ).
).
①证明: ;
;
②若三个零点均属于区间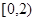 ,求
,求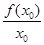 的取值范围.
的取值范围.
相关知识点
推荐套卷
(本小题满分13分)已知函数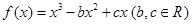 ,其图象记为曲线
,其图象记为曲线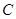 .
.
(Ⅰ)若 在
在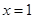 处取得极值为
处取得极值为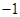 ,求
,求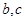 的值;
的值;
(Ⅱ)若 有三个不同的零点,分别为
有三个不同的零点,分别为 ,且
,且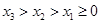 ,过点
,过点 作曲线
作曲线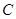 的切线,切点为
的切线,切点为 (点
(点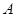 异于点
异于点 ).
).
①证明: ;
;
②若三个零点均属于区间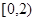 ,求
,求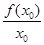 的取值范围.
的取值范围.