（本小题满分13分）已知抛物线的顶点在原点，焦点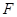
在
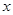轴上，且抛物线上横坐标为1的点到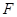的距离为2 ，过点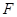的直线交抛物线于
，
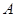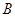两点．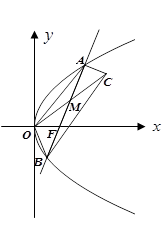
（Ⅰ）求抛物线的方程；
（Ⅱ）若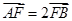
，求直线
的斜率；
（Ⅲ）设点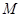
在线段上运动，原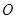点
关于点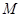的对称点为
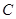，求四边形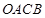
面积的最小值．
相关试题
满足
，且
在复平面上对应的点在第二、四象限的角平分线上，若
，求
的值。
中，
，且前
项的算术平均数等于第
倍（
）．
，观察下列不等式：
，
，
，请你猜测
满足的不等式，并用数学归纳法加以证明．
，
满足
，且
为纯虚数，求证：
为实数．相关知识点
推荐套卷
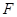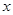（本小题满分13分）已知抛物线的顶点在原点，焦点在轴上，且抛物线上横坐标为1的点到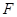的距离为2 ，过点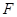的直线交抛物线于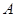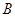，两点．
（Ⅰ）求抛物线的方程；
（Ⅱ）若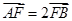，求直线的斜率；
（Ⅲ）设点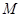在线段上运动，原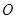点关于点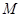的对称点为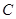，求四边形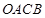面积的最小值．
粤公网安备 44130202000953号