(本小题满分12分)如图,点C是以AB为直径的圆O上不与A、B重合的一个动点,S是圆O所在平面外一点,且总有SC⊥平面ABC,M是SB的中点,AB=SC=2.
(Ⅰ)求证:OM⊥BC;
(Ⅱ)当四面体S-ABC的体积最大时,设直线AM与平面ABC所成的角为 ,二面角B-SA-C的大小为
,二面角B-SA-C的大小为 ,分别求
,分别求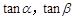 的值.
的值.
相关知识点
推荐套卷
(本小题满分12分)如图,点C是以AB为直径的圆O上不与A、B重合的一个动点,S是圆O所在平面外一点,且总有SC⊥平面ABC,M是SB的中点,AB=SC=2.
(Ⅰ)求证:OM⊥BC;
(Ⅱ)当四面体S-ABC的体积最大时,设直线AM与平面ABC所成的角为 ,二面角B-SA-C的大小为
,二面角B-SA-C的大小为 ,分别求
,分别求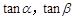 的值.
的值.