我市某校在推进新课改的过程中，开设的体育选修课有：A：篮球，B：足球，C：排球，D：羽毛球，E：乒乓球，学生可根据自己的爱好选修一门，学校李老师对某班全班同学的选课情况进行调查统计，制成了两幅不完整的统计图（如图）．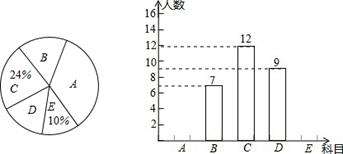
（1）请你求出该班的总人数，并补全频数分布直方图；
（2）该班班委4人中，1人选修篮球，2人选修足球，1人选修排球，李老师要从这4人中人选2人了解他们对体育选修课的看法，请你用列表或画树状图的方法，求选出的2人恰好1人选修篮球，1人选修足球的概率．
相关试题
甲、乙两名同学进入初三后，某科6次考试成绩如图：（1）请根据下图填写如表：
| |
平均数 |
方差 |
中位数 |
众数 |
极差 |
| 甲 |
75 |
|
75 |
|
|
| 乙 |
|
33.3 |
|
|
15 |
（2）请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析：
①从平均数和方差相结合看；
②从折线图上两名同学分数的走势上看，你认为反映出什么问题？
如图，在△ABC中,AB=AC，DE是边AB垂直平分线交AB于E，交AC于D，连结BD。
（1）若∠A=40°，求∠DBC的度数。
（2）若△BCD的周长为12cm，△ABC的周长为18cm，求BE的长。
粤公网安备 44130202000953号