如图,已知抛物线y= —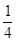 x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
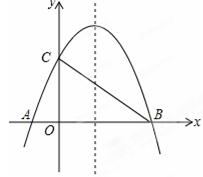
(1)求抛物线的解析式及其对称轴方程;
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;
(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;
(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由
相关知识点
推荐套卷
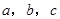 各应是多少吗?第
各应是多少吗?第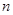 组呢?
组呢?
 BC,F为CD的中点,连接AF、AE,问△AEF是什么三角形?请说明理由.
BC,F为CD的中点,连接AF、AE,问△AEF是什么三角形?请说明理由.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号