已知 在平面直角坐标系中的位置如图所示。
在平面直角坐标系中的位置如图所示。
(1)分别写出图中点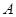 和点
和点 的坐标;
的坐标;
(2)画出 绕点A按逆时针方向旋转90°后的
绕点A按逆时针方向旋转90°后的 ;
;
(3)在(2)的条件下,求点 旋转到点
旋转到点 所经过的路线长(结果保留
所经过的路线长(结果保留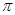 )
)
相关知识点
推荐套卷
已知 在平面直角坐标系中的位置如图所示。
在平面直角坐标系中的位置如图所示。
(1)分别写出图中点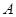 和点
和点 的坐标;
的坐标;
(2)画出 绕点A按逆时针方向旋转90°后的
绕点A按逆时针方向旋转90°后的 ;
;
(3)在(2)的条件下,求点 旋转到点
旋转到点 所经过的路线长(结果保留
所经过的路线长(结果保留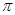 )
)