已知A（－2，0），B（2，0），动点P与A、B两点连线的斜率分别为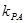
和
，
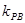且满足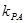·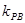="t" （t≠0且t≠－1）．
（1）求动点P的轨迹C的方程；
（2）当t＜0时，曲线C的两焦点为F1，F2，若曲线C上存在点Q使得∠F1QF2=120O，
求t的取值范围．
个，从中任取
次
求：
的平行线，把一枚半径
的硬币任意掷在这个平面上，求硬币不与任何一条平行线相碰的概率。
颗质地均匀的骰子，求点数和为
的概率
推荐套卷
已知A（－2，0），B（2，0），动点P与A、B两点连线的斜率分别为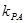和，
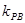且满足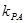·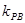="t" （t≠0且t≠－1）．
（1）求动点P的轨迹C的方程；
（2）当t＜0时，曲线C的两焦点为F1，F2，若曲线C上存在点Q使得∠F1QF2=120O，
求t的取值范围．
粤公网安备 44130202000953号