（本小题满分12分）如图，在四棱锥P—ABCD中，平面PAB⊥平面ABCD，AD∥BC，∠ABC＝90°，PA＝PB＝3，BC＝1，AB＝2，AD＝3，O是AB中点。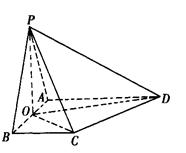
（1）证明CD⊥平面POC；
（2）求二面角C—PD—O的平面角的余弦值。
，
，若B⊆A，求实数m组成的集合．
若
，求
的值．
是一次函数，满足
，求
，
组成，若
，求x．
，x∈R，试讨论f（x）的奇偶性，并求f（x）的最小值．相关知识点
推荐套卷
（本小题满分12分）如图，在四棱锥P—ABCD中，平面PAB⊥平面ABCD，AD∥BC，∠ABC＝90°，PA＝PB＝3，BC＝1，AB＝2，AD＝3，O是AB中点。
（1）证明CD⊥平面POC；
（2）求二面角C—PD—O的平面角的余弦值。
粤公网安备 44130202000953号