已知AB＝AC，DB＝DE，∠BAC＝∠BDE＝α．
（1）如图1，α＝60°，探究线段CE与AD的数量关系，并加以证明；
（2）如图2，α＝120°，探究线段CE与AD的数量关系，并说明理由；
（3）如图3，结合上面的活动经验探究线段CE与AD的数量关系为__________ ．（直接写出答案）
相关试题
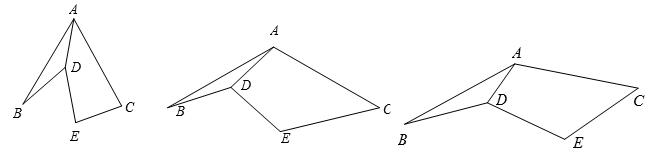
已知AB＝AC，DB＝DE，∠BAC＝∠BDE＝α．
（1）如图1，α＝60°，探究线段CE与AD的数量关系，并加以证明；
（2）如图2，α＝120°，探究线段CE与AD的数量关系，并说明理由；
（3）如图3，结合上面的活动经验探究线段CE与AD的数量关系为__________ ．（直接写出答案）
、
、
三条线路，从乙学校到丙学校有
、
二条线路．
.请你画出旋转后的△
．
粤公网安备 44130202000953号