如图,已知:抛物线C1: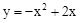 ,将抛物线C1向上平移m个单位(m>0)得抛物线C2,C2的顶点为G,与y轴交于M,点N是M关于x轴的对称点,点P(
,将抛物线C1向上平移m个单位(m>0)得抛物线C2,C2的顶点为G,与y轴交于M,点N是M关于x轴的对称点,点P(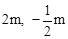 )在直线MG上。问:当m为何值时,在抛物线C2上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C2上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?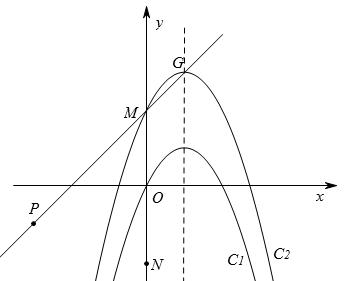
如图,已知:抛物线C1: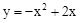 ,将抛物线C1向上平移m个单位(m>0)得抛物线C2,C2的顶点为G,与y轴交于M,点N是M关于x轴的对称点,点P(
,将抛物线C1向上平移m个单位(m>0)得抛物线C2,C2的顶点为G,与y轴交于M,点N是M关于x轴的对称点,点P(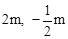 )在直线MG上。问:当m为何值时,在抛物线C2上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C2上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?