如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,反比例函数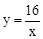 在第一象限内的图象经过点A,与BC交于点F,OB=
在第一象限内的图象经过点A,与BC交于点F,OB= ,BF=
,BF= BC。过点F作EF∥OB,交OA于点,点P为直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。
BC。过点F作EF∥OB,交OA于点,点P为直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。 
相关知识点
推荐套卷
如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,反比例函数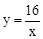 在第一象限内的图象经过点A,与BC交于点F,OB=
在第一象限内的图象经过点A,与BC交于点F,OB= ,BF=
,BF= BC。过点F作EF∥OB,交OA于点,点P为直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。
BC。过点F作EF∥OB,交OA于点,点P为直线EF上的一个动点,连接PA,PO。若以P、O、A为顶点的三角形是直角三角形,请求出所有点P的坐标。 