(2014年山东青岛10分)数学问题:计算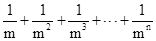 (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算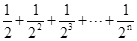 .
.
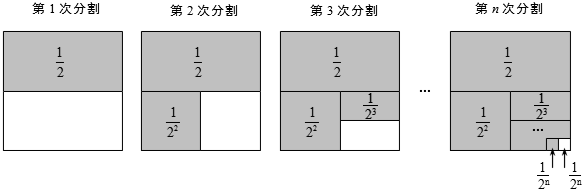
第1次分割,把正方形的面积二等分,其中阴影部分的面积为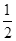 ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为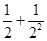 ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为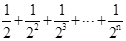 ,最后空白部分的面积是
,最后空白部分的面积是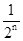 .
.
根据第n次分割图可得等式: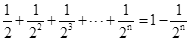 .
.
探究二:计算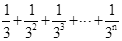 .
.
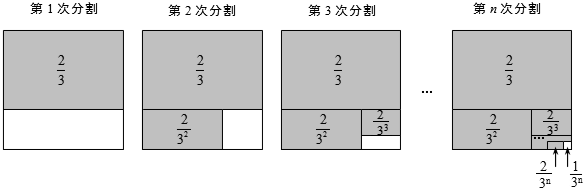
第1次分割,把正方形的面积三等分,其中阴影部分的面积为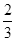 ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为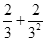 ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为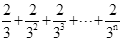 ,最后空白部分的面积是
,最后空白部分的面积是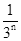 .
.
根据第n次分割图可得等式: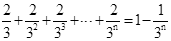 ,
,
两边同除以2,得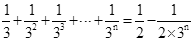 .
.
探究三:计算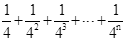 .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算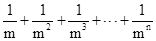 .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式: ,
所以,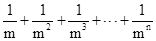 = .
= .
拓广应用:计算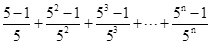 .
.
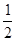 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
 轴上的一个动点, 当CM+DM的值最小时,求m的值.
轴上的一个动点, 当CM+DM的值最小时,求m的值.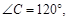 AC="BC," AB=6,O为AB的中点,且以O为圆心的半圆与AC,BC分别相切于点D,E;
AC="BC," AB=6,O为AB的中点,且以O为圆心的半圆与AC,BC分别相切于点D,E;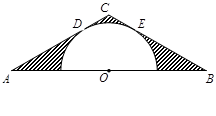
 粤公网安备 44130202000953号
粤公网安备 44130202000953号