如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.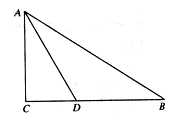
(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹);
(2)判断直线BC与⊙O的位置关系,并说明理由;
(3)若(1)中的⊙O与船边的另一个交点为E,AB=6,BD=2 ,求
,求 的弧长(结果保留根号和π).
的弧长(结果保留根号和π).
推荐套卷
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.
(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹);
(2)判断直线BC与⊙O的位置关系,并说明理由;
(3)若(1)中的⊙O与船边的另一个交点为E,AB=6,BD=2 ,求
,求 的弧长(结果保留根号和π).
的弧长(结果保留根号和π).