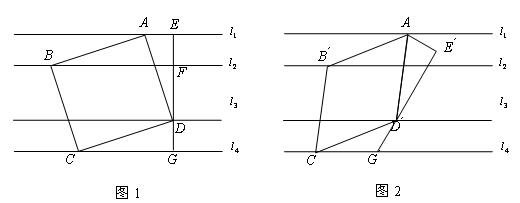
(2014年山东济南9分)如图1,有一组平行线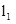 ∥
∥ ∥
∥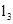 ∥
∥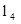 ,正方形ABCD的四个顶点分别在
,正方形ABCD的四个顶点分别在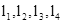 上,EG过点D且垂直于
上,EG过点D且垂直于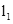 于点E,分别交
于点E,分别交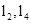 于点F,G,
于点F,G,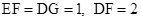 .
.
(1)AE= ,正方形ABCD的边长= ;
(2)如图2,将∠AEG绕点A顺时针旋转得到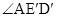 ,旋转角为
,旋转角为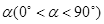 ,点
,点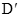 在直线
在直线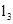 上,以
上,以 为边在的
为边在的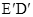 左侧作菱形
左侧作菱形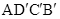 ,使点
,使点 分别在直线
分别在直线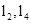 上.
上.
①写出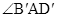 与
与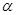 的函数关系并给出证明;
的函数关系并给出证明;
②若 ,求菱形
,求菱形 的边长.
的边长.
(2014年山东济南9分)如图1,有一组平行线 ∥
∥ ∥
∥ ∥
∥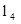 ,正方形ABCD的四个顶点分别在
,正方形ABCD的四个顶点分别在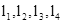 上,EG过点D且垂直于
上,EG过点D且垂直于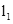 于点E,分别交
于点E,分别交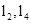 于点F,G,
于点F,G,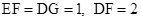 .
.
(1)AE= ,正方形ABCD的边长= ;
(2)如图2,将∠AEG绕点A顺时针旋转得到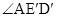 ,旋转角为
,旋转角为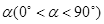 ,点
,点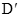 在直线
在直线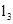 上,以
上,以 为边在的
为边在的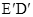 左侧作菱形
左侧作菱形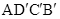 ,使点
,使点 分别在直线
分别在直线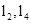 上.
上.
①写出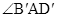 与
与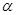 的函数关系并给出证明;
的函数关系并给出证明;
②若 ,求菱形
,求菱形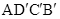 的边长.
的边长.
