(2014年湖北咸宁10分)如图1,P(m,n)是抛物线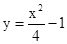 上任意一点,l是过点(0,﹣2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
上任意一点,l是过点(0,﹣2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
【探究】
(1)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= ;
【证明】
(2)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
【应用】
(3)如图2,已知线段AB=6,端点A,B在抛物线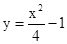 上滑动,求A,B两点到直线l的距离之和的最小值.
上滑动,求A,B两点到直线l的距离之和的最小值.

(2014年湖北咸宁10分)如图1,P(m,n)是抛物线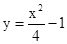 上任意一点,l是过点(0,﹣2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
上任意一点,l是过点(0,﹣2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
【探究】
(1)填空:当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= ;
【证明】
(2)对任意m,n,猜想OP与PH的大小关系,并证明你的猜想.
【应用】
(3)如图2,已知线段AB=6,端点A,B在抛物线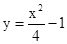 上滑动,求A,B两点到直线l的距离之和的最小值.
上滑动,求A,B两点到直线l的距离之和的最小值.
