（年福建三明14分）如图，在平面直角坐标系中，抛物线y=ax2+bx+4与x轴的一个交点为A（﹣2，0），与y轴的交点为C，对称轴是x=3，对称轴与x轴交于点B．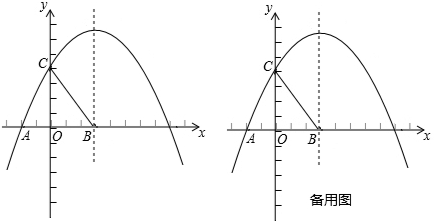
（1）求抛物线的函数表达式；
（2）经过B，C的直线l平移后与抛物线交于点M，与x轴交于点N，当以B，C，M，N为顶点的四边形是平行四边形时，求出点M的坐标；
（3）若点D在x轴上，在抛物线上是否存在点P，使得△PBD≌△PBC？若存在，直接写出点P的坐标；若不存在，请说明理由．
如图12，在△ABC中，∠ACB=
，AC=BC=2，M是边AC的中点，CH⊥BM于H.
试求sin∠MCH的值
求证：∠ABM=∠CAH；
若D是边AB上的点，且使△AHD为等腰三角形，请直接写出AD的长为________.
如图11，已知○为坐标原点，∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
求点B的坐标
若二次函数y=ax+bx+c的图象经过A、B、O三点，求此二次函数的解析式；
在(2)中的二次函数图象的OB段(不包括点O、B)上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标；若不存在，请说明理由。
在形如
的式子中，我们已经研究过两种情况：①已知a和b，求N，这是乘方运算；②已知b和N，求a，这是开方运算；
现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算。
定义：如果
（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记作：
，例如：求
，因为
＝8，所以=3；又比如∵
，∴
.根据定义计算：（本小题6分）
①
＝＿＿＿＿；②
=；
③如果
，那么x＝。设
则
(a＞0,a≠1,M、N均为正数),
∵
，∴
∴
，
即
这是对数运算的重要性质之一，进一步，我们还可以得出：
＝.（其中M1、M2、M3、……、Mn均为正数，a＞0，a≠1）（本小题2分）请你猜想：
(a＞0,a≠1,M、N均为正数).（本小题2分）
粤公网安备 44130202000953号