(年福建南平12分)如图,已知抛物线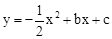 图象经过A(﹣1,0),B(4,0)两点.
图象经过A(﹣1,0),B(4,0)两点.
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.
(年福建南平12分)如图,已知抛物线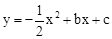 图象经过A(﹣1,0),B(4,0)两点.
图象经过A(﹣1,0),B(4,0)两点.
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.