（年江苏南通13分）如图，矩形ABCD中，AB=3，AD=4，E为AB上一点，AE=1，M为射线AD上一动点，AM=a（a为大于0的常数），直线EM与直线CD交于点F，过点M作MG⊥EM，交直线BC于G．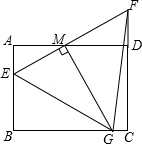
（1）若M为边AD中点，求证：△EFG是等腰三角形；
（2）若点G与点C重合，求线段MG的长；
（3）请用含a的代数式表示△EFG的面积S，并指出S的最小整数值．
相关试题
（1）问题发现
如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
填空：①∠AEB的度数为 ；②线段AD，BE之间的数量关系为 ．
（2）拓展探究
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．
如图，长方形纸片ABCD，AD∥BC，将长方形纸片折叠，使点D与点B重合，点C落在点C'处，折痕为EF，
（1）求证：BE＝BF．
（2）若∠ABE＝18°，求∠BFE的度数．
（3）若AB＝6，AD＝8，求AE的长．
粤公网安备 44130202000953号