(年湖南岳阳10分)如图,抛物线经过点A(1,0),B(5,0),C(0,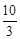 )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.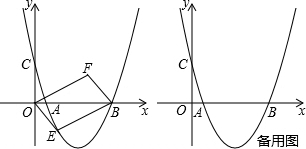
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.
(年湖南岳阳10分)如图,抛物线经过点A(1,0),B(5,0),C(0,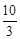 )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求平行四边形OEBF的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)是否存在这样的点E,使平行四边形OEBF为正方形?若存在,求E点,F点的坐标;若不存在,请说明理由.