（年广西南宁10分）如图甲，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上,∠AEF=90°，AE=EF，过点F作射线BC的垂线，垂足为H，连接AC.
（1）试判断BE与FH的数量关系，并说明理由；
（2）求证：∠ACF=90°；
（3）连接AF，过A，E，F三点作圆，如图乙. 若EC=4，∠CEF=15°，求
的长.
相关试题
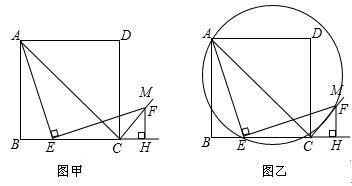
（年广西南宁10分）如图甲，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上,∠AEF=90°，AE=EF，过点F作射线BC的垂线，垂足为H，连接AC.
（1）试判断BE与FH的数量关系，并说明理由；
（2）求证：∠ACF=90°；
（3）连接AF，过A，E，F三点作圆，如图乙. 若EC=4，∠CEF=15°，求的长.
，其中
．
粤公网安备 44130202000953号