如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
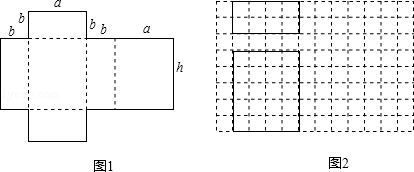
(1)这个几何体模型的名称是 .
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足 a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
相关知识点
推荐套卷
如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.

(1)这个几何体模型的名称是 .
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足 a2+b2﹣a﹣6b+10=0,求该几何体的表面积.
a2+b2﹣a﹣6b+10=0,求该几何体的表面积.