二次函数图象的顶点在原点O，经过点A（1，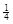
）；点F（0，1）在y轴上．直线y=﹣1与y轴交于点H．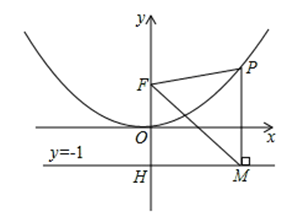
（1）求二次函数的解析式；
（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=﹣1交于点M，求证：FM平分∠OFP；
（3）当△FPM是等边三角形时，求P点的坐标．
的值:
ABCD的面积为20
，∠B=30°，AE⊥BC于E点，若BC=8
≈1.414，
≈1.732，求（
-
-2
）-
+
的值（精确到0.01）．
，b-c=2-
，b=4
，c=2
，求周长P．相关知识点
推荐套卷
二次函数图象的顶点在原点O，经过点A（1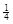，）；点F（0，1）在y轴上．直线y=﹣1与y轴交于点H．
（1）求二次函数的解析式；
（2）点P是（1）中图象上的点，过点P作x轴的垂线与直线y=﹣1交于点M，求证：FM平分∠OFP；
（3）当△FPM是等边三角形时，求P点的坐标．
粤公网安备 44130202000953号