(原创)已知集合M是满足下列性质的函数 的全体:存在非零常数T,对任意
的全体:存在非零常数T,对任意 ∈R,有
∈R,有 成立.
成立.
(1)函数 是否属于集合M?说明理由;
是否属于集合M?说明理由;
(2)若定义在R上的偶函数 满足
满足 ,求证:
,求证: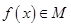 ;
;
(3)设函数 且
且 )的图象与
)的图象与 的图象有公共点,证明:
的图象有公共点,证明: ∈M;
∈M;
推荐套卷
(原创)已知集合M是满足下列性质的函数 的全体:存在非零常数T,对任意
的全体:存在非零常数T,对任意 ∈R,有
∈R,有 成立.
成立.
(1)函数 是否属于集合M?说明理由;
是否属于集合M?说明理由;
(2)若定义在R上的偶函数 满足
满足 ,求证:
,求证: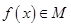 ;
;
(3)设函数 且
且 )的图象与
)的图象与 的图象有公共点,证明:
的图象有公共点,证明: ∈M;
∈M;