在三棱锥P－ABC中，D为AB的中点。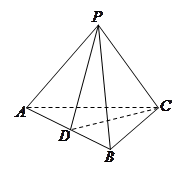
（1）与BC平行的平面PDE交AC于点E，判断点E在AC上的位置并说明理由如下：
（2）若PA＝PB，且△PCD为锐角三角形，又平面PCD⊥平面ABC，求证：AB⊥PC。
相关试题
及直线
．
为何值时，直线与椭圆有公共点？
，求直线的方程．
，离心率为0.6，求椭圆的标准方程。
对一切
恒成立, 求
的取值范围。
海里，则灯塔和轮船原来的距离为多少？
相关知识点
推荐套卷
在三棱锥P－ABC中，D为AB的中点。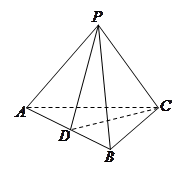
（1）与BC平行的平面PDE交AC于点E，判断点E在AC上的位置并说明理由如下：
（2）若PA＝PB，且△PCD为锐角三角形，又平面PCD⊥平面ABC，求证：AB⊥PC。
粤公网安备 44130202000953号