（本小题满分12分）为了研究某种细菌在特定环境下，随时间变化繁殖情况，得如下实验数据：
| 天数t（天） |
3 |
4 |
5 |
6 |
7 |
| 繁殖个数y（千个） |
2．5 |
3 |
4 |
4．5 |
6 |
（Ⅰ）求y关于t的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，预测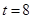
时，细菌繁殖个数．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，
．
．
取最值时的
的值；
，求下列各式的值：
；
．
．
(7分)
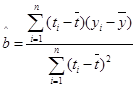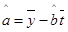，求sinθ和tanθ的值．推荐套卷
（本小题满分12分）为了研究某种细菌在特定环境下，随时间变化繁殖情况，得如下实验数据：
| 天数t（天） |
3 |
4 |
5 |
6 |
7 |
| 繁殖个数y（千个） |
2．5 |
3 |
4 |
4．5 |
6 |
（Ⅰ）求y关于t的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，预测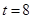时，细菌繁殖个数．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，．
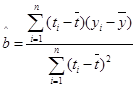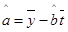粤公网安备 44130202000953号