(本小题满分12分)已知焦点在
轴上的椭圆C1：
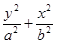=1经过A(1，0)点，且离心率为
．
(I)求椭圆C1的方程；
(Ⅱ)过抛物线C2：
(h∈R)上P点的切线与椭圆C1交于两点M、N，记线段MN与PA的中点分别为G、H，当GH与轴平行时，求h的最小值．
的最小正周期为
，最小值为
，图像过点
的解析式
且
的
的集合 。
为非零向量，且
，求
与
的夹角
。
和点
，其中
，若
,求
得值。
，计算
的值
，且
为第三象限角，求
及
的值。推荐套卷
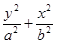(本小题满分12分)已知焦点在轴上的椭圆C1：=1经过A(1，0)点，且离心率为．
(I)求椭圆C1的方程；
(Ⅱ)过抛物线C2：(h∈R)上P点的切线与椭圆C1交于两点M、N，记线段MN与PA的中点分别为G、H，当GH与轴平行时，求h的最小值．
粤公网安备 44130202000953号