（本小题满分7分）选修4—2:矩阵与变换
在平面直角坐标系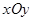
中，把矩阵
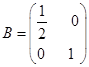确定的压缩变换
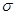与矩阵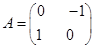
确定的旋转变换
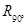进行复合，得到复合变换
．
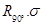（Ⅰ）求复合变换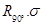的坐标变换公式；
（Ⅱ）求圆C：x2+ y2 =1在复合变换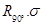的作用下所得曲线
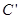的方程．
相关试题
]的一个特征值为2，其对应的一个特征向量为
=[
]．
]=[
]，求x，y的值．
的一个特征值λ1=3及对应的一个特征向量
=
．
所对应的变换把直线l：2x﹣y=3变换为自身，求M﹣1．
，求点M（﹣1，1）在矩阵A﹣1对应的变换作用下得到的点M′坐标．
（k≠0）的一个特征向量为α=
，A的逆矩阵A﹣1对应的变换将点（3，1）变为点（1，1）．求实数a，k的值．推荐套卷
（本小题满分7分）选修4—2:矩阵与变换
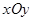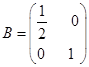在平面直角坐标系中，把矩阵确定的压缩变换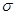与矩阵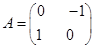确定的旋转变换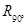进行复合，得到复合变换．
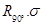（Ⅰ）求复合变换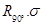的坐标变换公式；
（Ⅱ）求圆C：x2+ y2 =1在复合变换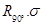的作用下所得曲线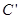的方程．
粤公网安备 44130202000953号