（本小题满分12分）某运动队拟在2015年3月份安排5次体能测试，规定：依次测试，只需有一次测试合格就不必参加后续的测试．已知运动员小刘5次测试每次合格的概率依次构成一个公差为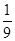
的等差数列，他第一次测试合格的概率不超过
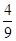，且他直到第二次测试才合格的概率为
．
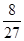（Ⅰ）求小刘第一次参加测试就合格的概率；
（Ⅱ）在小刘参加第一、第二次测试均不合格的前提下，记小刘参加后续测试的次数为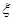
，求随机变量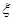的分布列和数学期望．
相关试题
，
且
的定义域； 
的奇偶性，并予以证明；
的定义域；
的值域；
，求
的单调递减区间。
在区间
上单调递减，求实数
的取值范围。
,
，
，（1）求
；（2）求
推荐套卷
（本小题满分12分）某运动队拟在2015年3月份安排5次体能测试，规定：依次测试，只需有一次测试合格就不必参加后续的测试．已知运动员小刘5次测试每次合格的概率依次构成一个公差为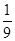的等差数列，他第一次测试合格的概率不超过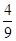，且他直到第二次测试才合格的概率为．
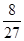（Ⅰ）求小刘第一次参加测试就合格的概率；
（Ⅱ）在小刘参加第一、第二次测试均不合格的前提下，记小刘参加后续测试的次数为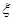，求随机变量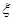的分布列和数学期望．
粤公网安备 44130202000953号