张华同学上学途中必须经过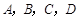
四个交通岗，其中在
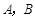岗遇到红灯的概率均为
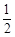，在
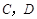岗遇到红灯的概率均为
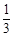．假设他在4个交通岗遇到红灯的事件是相互独立的，X表示他遇到红灯的次数．
（1）若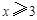
，就会迟到，求张华不迟到的概率；
（2）求EX．
相关试题
,求直线l的方程.相关知识点
推荐套卷
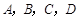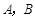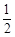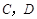张华同学上学途中必须经过四个交通岗，其中在岗遇到红灯的概率均为，在岗遇到红灯的概率均为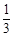．假设他在4个交通岗遇到红灯的事件是相互独立的，X表示他遇到红灯的次数．
（1）若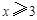，就会迟到，求张华不迟到的概率；
（2）求EX．
粤公网安备 44130202000953号