(本小题满分12分)已知函数f(x)=ax-l+lnx,其中a为常数.
(Ⅰ)当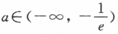 时,若f(x)在区间(0,e)上的最大值为一4,求a的值;
时,若f(x)在区间(0,e)上的最大值为一4,求a的值;
(Ⅱ)当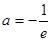 时,若函数
时,若函数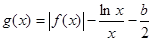 存在零点,求实数b的取值范围.
存在零点,求实数b的取值范围.
相关知识点
推荐套卷
(本小题满分12分)已知函数f(x)=ax-l+lnx,其中a为常数.
(Ⅰ)当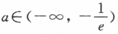 时,若f(x)在区间(0,e)上的最大值为一4,求a的值;
时,若f(x)在区间(0,e)上的最大值为一4,求a的值;
(Ⅱ)当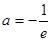 时,若函数
时,若函数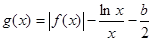 存在零点,求实数b的取值范围.
存在零点,求实数b的取值范围.