(本小题满分6分)如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.
(1)求CD与AB之间的距离;
(2)某人从车站A出发,沿折线A→D→C→B去超市B,求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米?
(参考数据:sin67°≈ ,cos67°≈
,cos67°≈ ,tan67°≈
,tan67°≈ ,sin37°≈
,sin37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈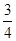 )
)
相关知识点
推荐套卷

 过定点M(1,1),则称此抛物线为定点抛物线。
过定点M(1,1),则称此抛物线为定点抛物线。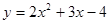 ,请你写出一个不同于小敏的答案;
,请你写出一个不同于小敏的答案;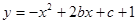 ,求该抛物线顶点纵坐标的值最小时的解析式,请你解答。
,求该抛物线顶点纵坐标的值最小时的解析式,请你解答。
 ,
,

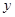 (米)和所经过的时间
(米)和所经过的时间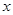 之间的函数图象如图所示。请根据图象回答下列问题:
之间的函数图象如图所示。请根据图象回答下列问题: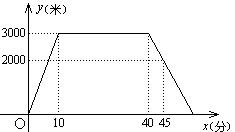
 粤公网安备 44130202000953号
粤公网安备 44130202000953号