九（一）班课题学习小组，为了了解大树生长状况，去年在学校门前点A处测得一棵大树顶点C的仰角为30°，树高5m；今年他们仍在原点A处测得大树D的仰角为37°，问这棵树一年生长了多少m？（参考数据：sin37°≈0．6，cos37°≈0．8，tan37°≈0．75，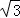
≈1．732）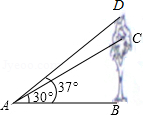
相关试题
九（一）班课题学习小组，为了了解大树生长状况，去年在学校门前点A处测得一棵大树顶点C的仰角为30°，树高5m；今年他们仍在原点A处测得大树D的仰角为37°，问这棵树一年生长了多少m？（参考数据：sin37°≈0．6，cos37°≈0．8，tan37°≈0．75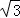，≈1．732）
与-0.76；（2）-
与-
；
与-3
与-│-
│；（4）-
与-│3.14│．
，b=-
，试比较a，b的大小．
与-0.626363．
粤公网安备 44130202000953号