（本小题满分14分）已知椭圆C：
（a＞b＞0）与y轴的交点为A，B（点A位于点B的上方），F为左焦点，原点O到直线FA的距离为
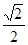b．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）设b=2，直线y=kx+4与椭圆C交于不同的两点M，N，求证：直线BM与直线AN的交点G在定直线上．
相关试题
(2)
：
上存在零点，求实数
的取值范围；
，当
时，
的值域为区间
，且
。推荐套卷
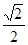（本小题满分14分）已知椭圆C：（a＞b＞0）与y轴的交点为A，B（点A位于点B的上方），F为左焦点，原点O到直线FA的距离为b．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）设b=2，直线y=kx+4与椭圆C交于不同的两点M，N，求证：直线BM与直线AN的交点G在定直线上．
粤公网安备 44130202000953号