（本小题满分为14分） 如图，过四棱柱
形木块上底面内的一点
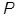和下底面的对角线
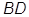将木块锯开，得到截面
.
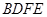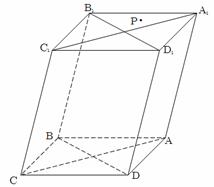
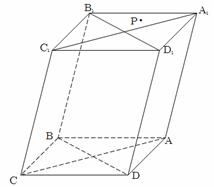
（1）请在木块的上表面作出过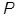的锯线
，并说明理由；
（2）若该四棱柱的底面为菱形，四边形
是矩形时，试证明：平面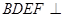
平面
.
相关试题
；
．
在
上的最大值是
，求
的值； 
，总存在
，使得
成立，求
在
上有解，求
的定义域为
，对于任意正实数
恒有
，且当
时，
的值；
的不等式
．
．
的最小值和最小正周期；
内角
的对边分别为
，且
，若向量
与
共线，求
的值．推荐套卷
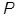（本小题满分为14分） 如图，过四棱柱形木块上底面内的一点和下底面的对角线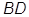将木块锯开，得到截面.
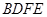（1）请在木块的上表面作出过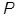的锯线，并说明理由；
（2）若该四棱柱的底面为菱形，四边形是矩形时，试证明：平面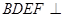平面.
粤公网安备 44130202000953号