袋中装着分别标有数字1,2,3,4,5的5个形状相同的小球.
(1)从袋中任取2个小球,求两个小球所标数字之和为3的倍数的概率;
(2)从袋中有放回的取出2个小球,记第一次取出的小球所标数字为x,第二次为y,求点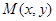 满足
满足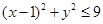 的概率.
的概率.
推荐套卷
袋中装着分别标有数字1,2,3,4,5的5个形状相同的小球.
(1)从袋中任取2个小球,求两个小球所标数字之和为3的倍数的概率;
(2)从袋中有放回的取出2个小球,记第一次取出的小球所标数字为x,第二次为y,求点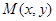 满足
满足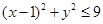 的概率.
的概率.