在上海世博会期间,小红计划对事先选定的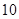 个场馆进行参观.在她选定的
个场馆进行参观.在她选定的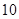 个场馆中,有
个场馆中,有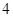 个场馆分布在
个场馆分布在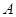 区,
区,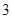 个场馆分布在
个场馆分布在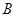 区,
区,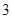 个场馆分布在
个场馆分布在 区.已知
区.已知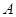 区的每个场馆的排队时间为
区的每个场馆的排队时间为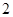 小时,
小时,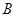 区和
区和 区的每个场馆的排队时间为
区的每个场馆的排队时间为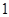 小时.参观前小红因事只能从这
小时.参观前小红因事只能从这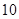 个场馆中随机选定
个场馆中随机选定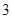 个场馆进行参观.
个场馆进行参观.
(Ⅰ)求小红每个区都参观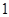 个场馆的概率;
个场馆的概率;
(Ⅱ)设小红排队时间总和为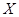 (小时),求随机变量
(小时),求随机变量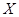 的分布列和数学期望
的分布列和数学期望 .
.
推荐套卷
在上海世博会期间,小红计划对事先选定的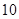 个场馆进行参观.在她选定的
个场馆进行参观.在她选定的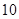 个场馆中,有
个场馆中,有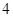 个场馆分布在
个场馆分布在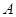 区,
区,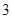 个场馆分布在
个场馆分布在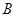 区,
区,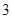 个场馆分布在
个场馆分布在 区.已知
区.已知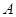 区的每个场馆的排队时间为
区的每个场馆的排队时间为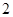 小时,
小时,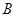 区和
区和 区的每个场馆的排队时间为
区的每个场馆的排队时间为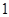 小时.参观前小红因事只能从这
小时.参观前小红因事只能从这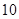 个场馆中随机选定
个场馆中随机选定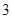 个场馆进行参观.
个场馆进行参观.
(Ⅰ)求小红每个区都参观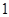 个场馆的概率;
个场馆的概率;
(Ⅱ)设小红排队时间总和为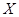 (小时),求随机变量
(小时),求随机变量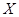 的分布列和数学期望
的分布列和数学期望 .
.