（本小题12分）六名学生需依次进行身体体能和外语两个项目的训练及考核 每个项目只有一次补考机会，补考不合格者不能进入下一个项目的训练（即淘汰），若每个学生身体体能考核合格的概率是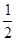
，外语考核合格的概率是
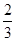，假设每一次考试是否合格互不影响.
（1）求某个学生不被淘汰的概率.
（2）求6名学生至多有两名被淘汰的概率
（3）假设某学生不放弃每一次考核的机会，用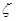
表示其参加补考的次数，求随机变量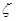的分布列和数学期望.
相关试题
的三个内角，向量
,
，且
．
的值．
的两个极值点，且
。
，并求出a的取值范围.
.
,证明:当
且x1<0时, 
.
满足
，当2≤x≤6时，
。
与
的大小
其中a>0，e为自然对数的底数。
的单调区间；
中，底面ABCD是正方形，侧棱
底面ABCD，
，E是PC的中点.
平面
；（2）求EB与底面ABCD所成的角的正切值.
推荐套卷
（本小题12分）六名学生需依次进行身体体能和外语两个项目的训练及考核 每个项目只有一次补考机会，补考不合格者不能进入下一个项目的训练（即淘汰），若每个学生身体体能考核合格的概率是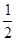，外语考核合格的概率是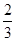，假设每一次考试是否合格互不影响.
（1）求某个学生不被淘汰的概率.
（2）求6名学生至多有两名被淘汰的概率
（3）假设某学生不放弃每一次考核的机会，用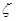表示其参加补考的次数，求随机变量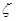的分布列和数学期望.
粤公网安备 44130202000953号