某市举行的一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
(Ⅰ)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(Ⅱ)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望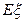 .
.
推荐套卷
某市举行的一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
(Ⅰ)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(Ⅱ)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望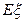 .
.