某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如下茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.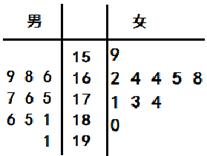
(Ⅰ)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;
(Ⅱ)求这5名队员中,恰好男女“高个子”各1名队员的概率.
推荐套卷
某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如下茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.
(Ⅰ)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;
(Ⅱ)求这5名队员中,恰好男女“高个子”各1名队员的概率.