(本小题满分13分)已知点列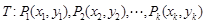 (
(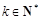 ,
,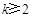 )满足
)满足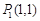 ,且
,且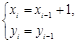 与
与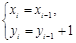 (
(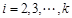 ) 中有且仅有一个成立.
) 中有且仅有一个成立.
(Ⅰ)写出满足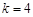 且
且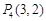 的所有点列;
的所有点列;
(Ⅱ) 证明:对于任意给定的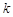 (
(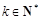 ,
,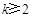 ),不存在点列
),不存在点列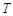 ,使得
,使得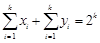 ;
;
(Ⅲ)当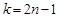 且
且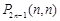 (
(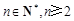 )时,求
)时,求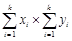 的最大值.
的最大值.
推荐套卷
(本小题满分13分)已知点列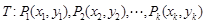 (
(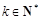 ,
,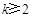 )满足
)满足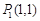 ,且
,且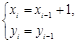 与
与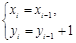 (
(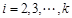 ) 中有且仅有一个成立.
) 中有且仅有一个成立.
(Ⅰ)写出满足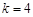 且
且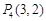 的所有点列;
的所有点列;
(Ⅱ) 证明:对于任意给定的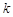 (
(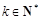 ,
,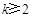 ),不存在点列
),不存在点列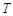 ,使得
,使得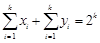 ;
;
(Ⅲ)当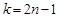 且
且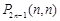 (
(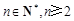 )时,求
)时,求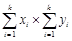 的最大值.
的最大值.