(本小题满分13分)已知椭圆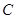 的两个焦点的坐标分别为
的两个焦点的坐标分别为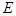
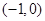 ,
,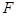
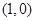 ,并且经过点(
,并且经过点(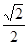 ,
,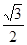 ),M、N为椭圆
),M、N为椭圆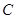 上关于
上关于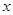 轴对称的不同两点.
轴对称的不同两点.
(1)求椭圆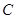 的标准方程;
的标准方程;
(2)若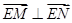 ,试求点
,试求点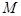 的坐标;
的坐标;
(3)若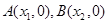 为
为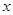 轴上两点,且
轴上两点,且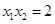 ,试判断直线
,试判断直线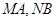 的交点
的交点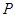 是否在椭圆
是否在椭圆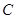 上,并证明你的结论.
上,并证明你的结论.
推荐套卷
(本小题满分13分)已知椭圆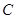 的两个焦点的坐标分别为
的两个焦点的坐标分别为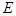
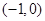 ,
,
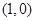 ,并且经过点(
,并且经过点(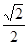 ,
,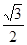 ),M、N为椭圆
),M、N为椭圆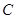 上关于
上关于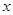 轴对称的不同两点.
轴对称的不同两点.
(1)求椭圆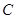 的标准方程;
的标准方程;
(2)若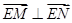 ,试求点
,试求点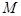 的坐标;
的坐标;
(3)若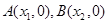 为
为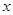 轴上两点,且
轴上两点,且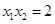 ,试判断直线
,试判断直线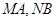 的交点
的交点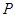 是否在椭圆
是否在椭圆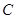 上,并证明你的结论.
上,并证明你的结论.