（本小题满分12分）如图，在四棱锥P－ABCD中，底面是直角梯形ABCD，其中AD⊥AB，CD∥AB，AB＝4，CD＝2，侧面PAD是边长为2的等边三角形，且与底面ABCD垂直，E为PA的中点．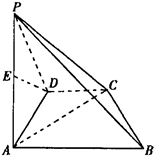
（Ⅰ）求证：DE∥平面PBC；
（Ⅱ）求三棱锥A－PBC的体积．
轴为对称轴，过焦点且垂直于对称轴的弦长为
，求抛物线的方程。
上一点到焦点的距离为
，求该点的坐标。
，求抛物线的方程。
，过点
引一弦，使它恰好在点
被平分，求这条弦所在的直线的方程。
，点
在圆周
上，求使
取最小值时点相关知识点
推荐套卷
（本小题满分12分）如图，在四棱锥P－ABCD中，底面是直角梯形ABCD，其中AD⊥AB，CD∥AB，AB＝4，CD＝2，侧面PAD是边长为2的等边三角形，且与底面ABCD垂直，E为PA的中点．
（Ⅰ）求证：DE∥平面PBC；
（Ⅱ）求三棱锥A－PBC的体积．
粤公网安备 44130202000953号