某高校共有学生15 000人,其中男生10 500人,女生4 500人,为调查该校学生每周平均体育运动的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4], (4,6], (6,8], (8,10], (10,12],估计该校学生每周平均体育运动时间超过4小时的概率;
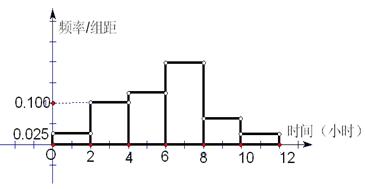
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附:

P(K2≥k0)
|
0.10
|
0.05
|
0.010
|
0.005
|
k0
|
2.706
|
3.841
|
6.635
|
7.879
|