（本小题满分12分）在△ABC中，角A，B，C的对边分别为a，b，c，已知c＝2，向量m＝（c，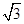
b），
n＝（cosC，sinB），且m∥n．
（Ⅰ）求角C的大小；
（Ⅱ）若sin（A＋B），sin2A，sin（B－A）成等差数列，求边a的大小．
相关试题
，
，
的定义域为
的值；
在区间
的取值范围。
.若
的定义域为
，求实数
的取值范围.
．
，求该三角形内切圆半径的取值范围。
的前
项和为
，已知对任意的
，点
均在函数
且
均为常数）的图像上．
的值；
时，记
，求数列
的前
．
，点
在函数
的图像上，（其中
）
是等比数列；
，求
及数列
的通项．推荐套卷
（本小题满分12分）在△ABC中，角A，B，C的对边分别为a，b，c，已知c＝2，向量m＝（c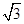，b），
n＝（cosC，sinB），且m∥n．
（Ⅰ）求角C的大小；
（Ⅱ）若sin（A＋B），sin2A，sin（B－A）成等差数列，求边a的大小．
粤公网安备 44130202000953号