猜想与证明：
如图1摆放矩形纸片ABCD与矩形纸片ECGF，使B、C、G三点在一条直线上，CE在边CD上，连接AF，若M为AF的中点，连接DM、ME，试猜想DM与ME的关系，并证明你的结论．
拓展与延伸：
（1）若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为 ．
（2）如图2摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF的中点，试证明（1）中的结论仍然成立．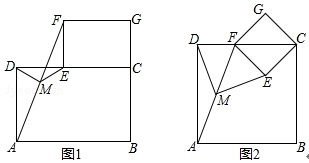
,求原长方形的宽。
、
和∠β（如图），利用直尺和圆规作ΔABC，使BC=
,其中
.
相关知识点
推荐套卷
粤公网安备 44130202000953号