某小区想利用一矩形空地 建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
,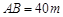 ,且
,且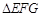 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一条直线交
作一条直线交 于
于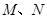 ,从而得到五边形
,从而得到五边形 的市民健身广场.
的市民健身广场.
(Ⅰ)假设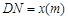 ,试将五边形
,试将五边形 的面积
的面积 表示为
表示为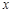 的函数,并注明函数的定义域;
的函数,并注明函数的定义域;
(Ⅱ)问:应如何设计,可使市民健身广场的面积最大?并求出健身广场的最大面积.
推荐套卷
某小区想利用一矩形空地 建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
,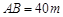 ,且
,且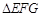 中,
中, ,经测量得到
,经测量得到 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点 作一条直线交
作一条直线交 于
于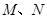 ,从而得到五边形
,从而得到五边形 的市民健身广场.
的市民健身广场.
(Ⅰ)假设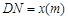 ,试将五边形
,试将五边形 的面积
的面积 表示为
表示为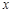 的函数,并注明函数的定义域;
的函数,并注明函数的定义域;
(Ⅱ)问:应如何设计,可使市民健身广场的面积最大?并求出健身广场的最大面积.